Compass navigation

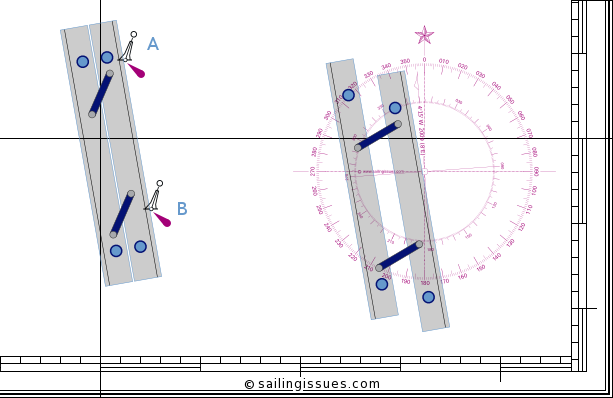
Marine compass

In China compasses have been in use since the Han dynasty (2nd century BCE to 2nd century CE) when they were referred to as “south-pointers”. However at first these magnets were only used for geomancy much like in the art of Feng Shui. Eventually, during the Sung dynasty (1000 CE) many trading ships were then able to sail as far as Saudi Arabia using compasses for marine navigation. Between 1405 and 1433, Emperor Chu Ti's Treasure Fleet of the Dragon Throne ruled the entire South Pacific and the Indian Ocean, a territory that ranges from Korea and Japan to the Eastern coast of Africa.
At this time Western mariners were still rather ignorant of the navigational use of the magnet. Petrus Perigrinus van Maricourt wrote a first treatise on the magnet itself: “De Magnete” (1269). And though its nautical use was already mentioned in 1187 by the English monk Alexander Neckham, the use onboard only came about around the 13th and 14th century in the Mediterranean Sea.
Much later, in 1545, Pedro de Medina (Sevilla 1493-1567) wrote the Spanish standard work “Arte de Navegar” on marine compass navigation. This masterpiece was first translated in Dutch (1580) and was -O Irony- used by Jacob van Heemskerk when the Dutch destroyed the Spanish fleet near Gibraltar in 1607. The drawback was of course Van Heemskerk's own death during this victory.

Magnetic Variation

In the fin-de-siècle of the sixteenth century mariners believed that the magnetic north pole coincided with the geographic north pole. Any suggestion otherwise had been denied by Pedro de Medina.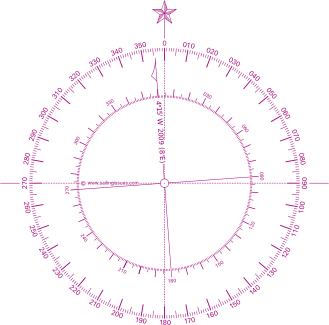 Magnetic observations made by explorers in subsequent decades showed however that these suggestions were true. But it took until the early nineteenth century, to pinpoint the magnetic north pole somewhere in Arctic Canada (78° N , 104° W). From then on the angle between the true North and the Magnetic North could be precisely corrected for. This correction angle is called magnetic variation or declination.
It is believed that the Earth's magnetic field is produced by electrical currents that originate in the hot, liquid, outer core of the rotating Earth. The flow of electric currents in this core is continually changing, so the magnetic field produced by those currents also changes. This means that at the surface of the Earth, both the strength and direction of the magnetic field will vary over the years. This gradual change is called the secular variation of the magnetic field. Therefore, variation changes not only with the location of a vessel on the earth but also varies in time.
The correction for magnetic variation for your location is shown on the nearest! nautical chart's compass rose. In this example we find a variation of 4° 15' W in 2009, with an indicated annual correction of 0° 08' E. Hence, in 2011 this variation is estimated to be 3° 59', almost 4° West. This means that if we sail 90° on the chart (the true course), the compass would read 94°.
Another example: let's say the compass rose gives a variation of 2° 50' E in 2007, with a correction of 0° 04' E per year. In 2009 this variation is estimated to be 2° 58', almost 3° East. Now, if we sail 90° on the chart, the compass would read 87°.

Correcting for variation

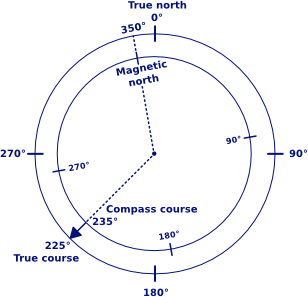These overlayed compass roses show the difference between true north and magnetic north when the magnetic variation is 10° West. From the image we find: tc = cc + var
in which “cc” and “tc” stand for “compass course” and “true course”, respectively.
To convert a true course into a compass course we need first assign a “-” to a Western and a “+” to a Eastern variation. Note that this makes sense! because of the clockwise direction of the compass rose. Here, the inner circle is turned 10° anticlockwise, hence -10°.
Now, use the same but re-written equation:
cc = tc - var
235° = 225° - (-10°)
So, to sail a true course of 225°, the helmsman has to steer a compass course of 235°.

To convert a compass course into a true course we can use the original equation. If we have steered a compass course of 200°, we have to plot a true course of 203° in the chart if the variation is 3° East or a true course of 190° if the variation is 10° West.

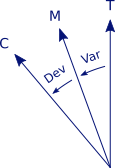
Magnetic deviation

Magnetic deviation is the second correctable error. The deviation error is caused by magnetic forces within your particular boat. Pieces of metal, such as an engine or an anchor, can cause magnetic forces. And also stereo and other electric equipment or wiring, if too close to the compass, introduce errors in compass heading. Furthermore, the deviation changes with the ship's heading, resulting in a deviation table as shown below. The vertical axis states the correction in degrees West or East, where East is again positive.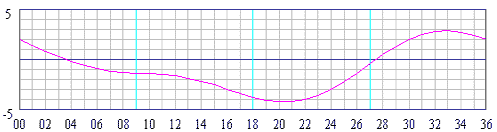


The horizontal axis states the ship's heading in degrees divided by ten. Thus, when you sail a compass course of 220°, the deviation is 4° W. (Note, that on most modern sailing yachts the deviation is usually not larger than 3°). When a compass is newly installed it often shows larger deviations than this and needs compensation by carefully placing small magnets around the compass. It is the remaining error that is shown in your deviation table.
You can check your table every now and then by placing your boat in the line of a pair of leading lights and turning her 360 degrees.

Correcting for both deviation and variation

Converting a compass course into a true course, we can still use our equation but we need to add the correction for deviation:
cc + var + dev = tc

• Example 1: The compass course is 330°, the deviation is +3° (table) and the variation is +3° (chart);
  330° cc + 3° var + 3° dev = ?° tc
  giving a true course of 336° which we can plot in our chart
  
• Example 2: The compass course is 220°, the deviation is -4° (table) and the variation is still +3° (chart).
  220° cc + 3° var + -4° dev = ?° tc
  giving a true course of 219°.
• Example 3: The compass course is still 220°, therefore the deviation is still -4° (table) but let's use a variation of -10° this time.
  220° cc + -10° var + -4° dev = ?° tc
  giving a true course of 206°.

Converting a true course into a compass course is a little less straight forward, but it is still done with the same equation.

• Example 4: The true course from the chart is 305° and the variation is +3° (chart), yet we don't know the deviation;
  ?° cc + 3° var + ?° dev = 305° tc
  Luckily, we can rewrite this so this reads:
  cc + dev = 305° tc - + 3° var = 302°
  In plain English: the difference between the true course and the variation (305 - + 3) = 302 should also be the summation of the compass course and the deviation. So, we can tell our helms person to steer 300°, since with a cc of 300° we have a deviation of +2° (As can be deduced from the deviation table above).
• Example 5: The true course from the chart is 150° and we have a Western variation of 7 degrees (-7°). We will use the rewritten equation to get:
  150° tc - - 7° var = cc + dev = 157°
  From the deviation table we find a compass course of 160° with a deviation of -3°.
  Voilà!

Magnetic course

   © sailingissues.com   

The magnetic course (mc) is the heading after magnetic variation has been considered, but without compensation for magnetic deviation. This means that we are dealing with the rewritten equation from above:
tc - var = cc + dev = mc. Magnetic courses are used for three reasons:

1. To convert a true course into a compass course like we saw in the last paragraph.
2. On vessels with more than one steering compass, also more deviation tables are in use; hence only a magnetic or true course is plotted in the chart.
3. Bearings taken with a handheld compass often don't require a correction for deviation, and are therefore useful to plot in the chart as magnetic courses.

Note, that the actual course lines the navigator draws in the chart are always true courses! These can subsequently be labeled with the true course or the corresponding magnetic or compass course if appropriate.

Some useful data in Youtube about Marine Radio related

http://www.youtube.com/watch?v=hlt4c-Lh2aU&feature=related

http://www.youtube.com/watch?v=ga6WdGkaeNM&feature=related

Nautical charts

Projections

The nautical chart is a 2-dimensional representation of a 3-dimensional world. And although this results in various distortions, as long as two requirements are met we can use this image for navigational purposes.

1. The angles between three objects in the chart should be the same as the angles between the real objects which they represent.
2. A straight course should appear as a straight line in the chart.

To fulfil these demands a nautical chart requires parallels and meridians that are both straight and parallel. Moreover, the meridians will need to be perpendicular to the parallels.
A well known method to create such a chart is called the Mercator projection after Gerard “Mercator” Kremer, a Flemish scholar who studied in 's Hertogenbosch (the Netherlands) and Leuven (now Belgium) and who invented his famous projection in 1569. The Mercator chart was designed for sailors and can be constructed by wrapping a cylinder around the planet so that it touches the equator. On this cylinder the surface of the earth is projected and finally the cylinder is cut open to yield the 2-dimensional chart.
But where the meridians converge on the globe they run parallel in the projection (see chart below), indicating the distortion. Look, for example, at a high parallel. The length of such a parallel on the globe is much smaller than the equator. Yet, on the chart they have exactly the same length creating a distortion which gets bigger nearer to the poles. The figure below shows the construction of the Mercator projection. From this it is clear that only the vertical scales should be used for measuring distances.
Click on the world map on the right to see the distortions of a Mercator projection. Each navy coloured circle/ellipse has a radius of 500 km.
The vertical scale depicted on the right demonstrates the distortion. The two little navy coloured markers have precisely the same size, the upper one measures only 0.64 degrees (= 38.4 nm) while the other measures 1.00 degrees (= 60 nm). So, distances (in degrees or in miles and minutes) should not only be read on the vertical scale, but also at approximately the same height. The horizontal scale is only valid for one latitude in the chart and can therefore only be used for the coordinates (a point, but not a line). If you divide the surface of the earth in eight pieces, and lift one out and project it, you end up with the figure below.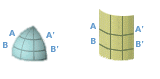 The result is that both A-A' and B-B' are now as long as the bottom of the chart and are “too long”.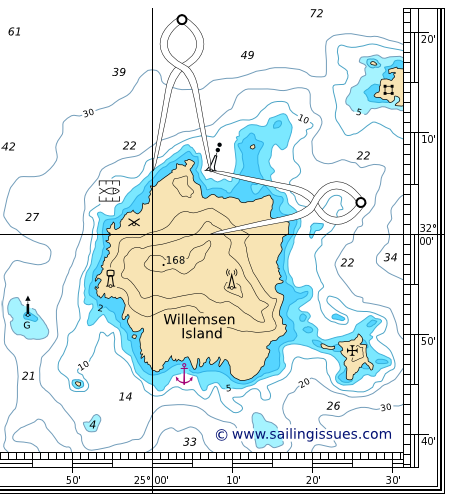
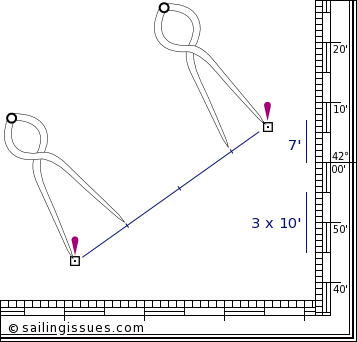But there are of course other projections in use by sailors. An important one is the Stereographic projection, which is constructed by projecting on a flat plane instead of a cylinder. On this chart parallels appear as slightly curved and also the meridians converge at high latitudes. So, strictly speaking, a straight course will not appear as a straight line in the chart, but the parallels remain perpendicular to the meridians. Most often, distortions are scarcely noticed when this projection is used to chart a small area. Like the Mercator projection, the vertical scale represents a meridian and should be used for measuring distances.
Another projection is the Gnomeric projection on which the meridians are again converging. But most importantly, the parallels are arcs of a circle while great circles appear as straight lines. On a sphere the shortest route between A and B is not a straight line but an arc (part of a great circle). Though this is also true when you – for example – cross a little bay, we use for simplification a loxodrome (a handy straight line on your Mercator chart which does not reflect your shortest route). On a Gnomeric chart this same loxodrome is an arc, while your shortest route (a great circle) ends up as a straight line. Hence, the gnomeric projection is particularly useful when sailing great circles (like when you dabble in circumnavigation) and is beyond the scope of a coastal navigation course.

Organization of the chart

• Authority: The publisher responsible for the information in the chart – “British Admiralty Charts”.
• Title: The title gives a description of the area covered by the chart – “The Aegean Sea of Greece - Athens to Rhodes”.
• Number: Different chart types of the same area can be distinguished by the chart's number.
• Projection: Most likely the Mercator projection as described above. Charts covering small areas can be constructed by stereographic projection.
• Scale: For example: 1:193.000. But since the chart is distorted this holds only for one specific latitude in the Mercator chart. The scale indicates how detailed the chart is (here 1 cm on the chart represents 193000 cm on earth).
• Horizontal geodetic datum: The definition of the relationship between the ellipsoid adopted as the model of the Earth's shape, and the Earth itself. Though there are hundreds of datums in use, most are only locally valid.
  Yet, the WGS-84 datum is global in scope and positions obtained by satellite navigation systems are usually referred to this datum. Therefore, a correction needs to be applied to a WGS-84 GPS position to agree with charts using other horizontal datums. For example to correct WGS-84 to the European datum, add 0,06'N , 0,04'E (style guide) to the WGS-84 position indicated by the GPS. Fortunately, most GPS receivers may be set to display positions in several other datums besides WGS-84 and perform the calculations for you.
• Chart sounding datum: The tidal datum to which soundings and drying heights on a chart are referred. Often shortened to “chart datum” when it is clear that reference is not being made to a horizontal datum. Chart sounding datums are also used as reference for heights (lighthouses, mountains, bridges). Multiple datums can be used in one chart: L.A.T. for soundings and M.L. for heights.
• Soundings & height units: Soundings and heights can be stated in - for example - metres, feet or fathoms. Today all charts worldwide are metric, except for USA Hydrographic Office charts, which sometimes still use feet instead of the international standard.
• Horizontal scale: Natural scale at for example 40° 15,3' S latitude where the horizontal scale can be used for measuring distances and where the chart scale is true.
• GPS compatibility: Most charts neither have the precision nor the resolution to fully use the (differential) GPS positioning potential. Moreover, still plenty of charts result from surveys done in the 19th century.
  Also, GPS data often requires a correction for a local horizontal chart datum before it can be used in the chart.
• Corrections & edition: The chart is for example a 2009 edition but is - when properly corrected - still valid in 2012. Corrections are published continuously and the changes made should be mentioned in the bottom left corner of the chart.

Information in the chart

• Depths reduced to chart datum: A sounding like 3₅ indicates 3½ metres of water under Lowest Astronomical Tide (when the chart datum is “L.A.T.”). An underlined sounding like 0₄ indicates a height of 40 cm above L.A.T..
  Heights above Chart Datum on drying areas are given in metres and decimetres. The metres figure is underlined.
  Depths are given from 0.1 to 20.9 in metres and decimetres, and from 21 to 31 in metres and half metres. Greater depths are rounded down to the nearest safest metre (for example, 32.7 metres is rounded down to 32 metres).
  The geographical position of a sounding is the centre of the depth figure.
• Isobaths: Lines connecting positions with the same depth: depth contours.
• Heights reduced to chart datum: Heights of for instance, lighthouses, mountains and cliffs are more often reduced to another datum such as Mean High Water (M.H.W.) or Mean High Water Spring.
• Tidal information: Details of both the vertical and the horizontal movement of the water is often included in the chart.
• Lighthouses, Buoys & marks: Lights, lateral and cardinal marks,
• Seabed qualities: Pebbles, seaweed, rocks, wrecks, pipelines, sand and other seabed characteristics for anchoring.
• Magnetic variation: The angle between the true North and the magnetic North varies in place and time. The local variation is indicated in the compass card, see
• Landmarks: conspicuous positions on the shore: Churches, radio masts, mountain tops, etc. that can be used for compass bearings and other means of navigation, these will be put to good use in 

Coordinates and positions

A pair of nautical dividers (single handed dividers) is used to obtain precise coordinates from the chart. This device enables you to take the distance between that particular position and the closest grid line. You then place the dividers on the scale with one end on this grid line, leaving the other end precisely at your coordinate. Do this twice to get both latitude and longitude at the scale on the edge of the chart.
Below are some examples.

	Danger mark 32° 06,3' N  ,  25° 07,3' E
	Fish farm 32° 04,4' N  ,  24° 54,7' E
	Anchorage 31° 46,0' N  ,  25° 04,0' E
	Church 31° 48,4' N  ,  25° 25,0' E
	Windmill 32° 01,0' N  ,  24° 57,8' E
	Castle 32° 14,2' N  ,  25° 29,6' E
	Water tower 31° 54,9' N  ,  24° 54,8' E
	Radio mast 31° 54,8' N  ,  25° 10,0' E
	Beacon green 31° 52,0' N  ,  24° 44,3' E

Plotting a position in the chart is done by reversing this method. Some chart symbols come with a little line and circle indicating the precise location, like the “Radio mast”, otherwise the center of the symbol is the precise location.
Another possible notation of 33° 28,5' E is 33° 28′ 30" E, which however doesn't easily allow for more precision like 33° 28,500' E does. Also note that in most countries a comma - and not a dot - is used as the decimal separator. So instead of 33° 28.500' E, the consensus notation for mariners is 33° 28,500' E.

Distances

To measure the distance between, for instance, these two oil rigs, we will again need our dividers. Remember, we can only use the vertical scale. We first take a convenient distance like 10' (10 nautical miles) on the vertical scale using the middle latitude. Then we start walking with the dividers from the southern oil rig to northern one. Finally, we adjust the dividers to measure the small remaining part at its own height, i.e. its own latitude.
The image shows that the total distance is 37 nautical miles.

Courses

   © sailingissues.com   

So, now we can measure distances and both plot and read out positions, but we also need directions. For example we need to find the course from safe-water buoy A to safe-water buoy B. To accomplish this we may use parallel rules as shown in this chart below:

First you line this instrument up with the two buoys. Then follows the intriguing part in moving the device to the compass rose without losing its alignment. Finally, when one of the rules is aligned with the heart of the compass card, you can read course A – B. In this example: 170°.
Besides the parallel rules there are other types of instruments available, notably the Breton plotter - also known as a Portland Course Plotter - which features an adjustable rose.

Selection of chart symbols

	Danger line in general
	Wreck, least depth unknown but usually deeper than 20 metres
	Visible wreck
	Wreck of which the mast(s) only are visible at Chart Datum
	Wreck, least depth known obtained by sounding only
	Wreck, least depth known, swept by wire drag or diver
or	Rock which covers and uncovers, height above Chart Datum
	Rock awash at the level of Chart Datum
	Underwater rock of unknown depth, dangerous to surface navigation
or	Underwater rock of known depth, dangerous to surface navigation
	Remains of a wreck, or other foul area, non-dangerous to navigation but to be avoided by vessels anchoring, trawling etc.
	Depth unknown, but considered to have a safe clearance to the depth shown
	Sounding of doubtful depth; Existence doubtful; Reported, but not confirmed
	Position approximate; Position doubtful
or	Wind turbine
	Chimney
	Tower; radio/television tower
	Monument
	Marina - boat harbour
	Mosque, minaret
	Silo
	Tanks
	Placeholder examples: Church (Ch)   Tower (Tr)   Hotel   Cupola (Cu)   Chimney (Chy). CAPITALS indicate that the landmark is conspicious.
	Quarrie, mine
	Major light; minor light
	Limit of safety zone around offshore installation
	Position of tabulated tidal stream data with designation “A”;   Tidal levels data “a”
	Green or black buoys (symbols filled black): G = Green ; B = Black
	Single coloured buoys other than green and black: Y = Yellow ; R = Red
	Multiple colours in horizontal bands, the colour sequence is from top to bottom
	Multiple colours in vertical or diagonal stripes, the darker colour is given first. W = White
	Lighted marks on multicoloured charts, GPS displays and chart plotters. A yellow coloured lobe indicates a White light! Also note that beacons (here the rightmost symbol with the green light) has an upright G, instead of an oblique G

   

 

Glossary

• Mercator projection: Most coastal nautical charts are constructed with this method. Angles are true and distances can be measured using the vertical scale.
• Stereographic projection: Used for chart covering small areas. Like the Mercator projection use the vertical scale to measure distances.
• Gnomeric projection: Used for vast areas. Great circles appear as straight lines on the chart.
• Great circle navigation: The shortest course on earth between two positions is a great circle; for circumnavigating and ocean crossings.
• Loxodrome: A line which makes the same angle with all meridians. Theoretically not the shortest route, but a handy straight line on a Mercator chart.
• Horizontal geodetic datum: Defines the relationship between the ellipsoid adopted as the model of the Earth's shape, and the Earth itself. Coordinates which refer to, for instance, AIA should be corrected before plotting them in a chart based on another horizontal datum. If your GPS receiver consistently disagrees with known positions by a constant amount and direction, then check that you have set it to display the correct horizontal datum.
• Chart sounding datum: The tidal datum (fictitious plane) to which soundings, heights, elevations and drying heights on a chart are referred.
• Vertical scale: Distances in nautical miles or minutes (') should be measured at the same latitude on the vertical scale.
• Corrections: Each chart is liable to corrections which are published by either a national body or the publisher of the nautical chart.